Fractal Analysis of the Distribution of Cave Lengths in Slovenia

Abstract

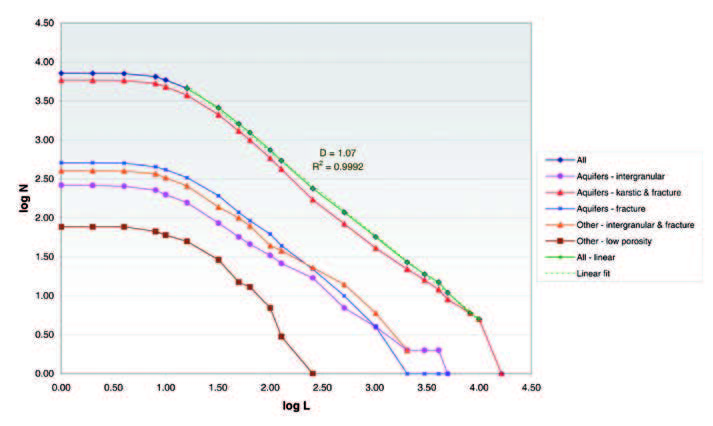
The lengths of the Slovenian caves follow the power-law distribution through several orders of magnitude, which implies that the caves can be considered as natural fractal objects. Fractal dimensions obtained from distribution of all caves are about 1.07, and vary within different tectonic and hydrogeological units. Some deviations from the ideal best fit line in log-log plots (i.e. lower and upper cut-off limits) can be explained by underestimation, as many very short caves are not registered. The study of tectonic and hydrogeological setting indicates that the greatest dimensions occur in the rocks with karstic-fracture and fracture porosity and the lowest in low-permeability rocks. Proximity to major tectonic structures shows a detectable effect on the cave length distribution, and the influence is greatest for the caves closer to the faults and thrust fronts. Dimensions are lower than those of fracture networks and faults, which can be most probably explained by flow channeling along the fracture networks, which causes the decrease of fractal dimension. The physical causes of power law scaling and variations in fractal dimensions (power law exponents) are still poorly understood, but the behaviour of fracture networks is believed to be caused by a scale-independent fractal fragmentation of the blocks, and during the process of forming the caves inherit some fractal geometrical properties of the networks.