Regular stalagmites: The theory behind their shape

Abstract

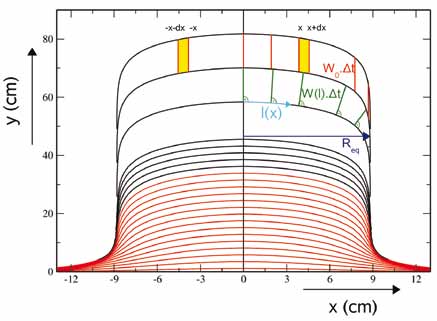
Under growth conditions constant in time stalagmites grow into an equilibrium shape, which is established, when all points of its surface are shifting by the same vertical distance during a time inter­val. Thereby is the recipitation rate in, is the calcium concentration of the supersatu­rated solution dripping to the apex of the stalagmite, and its equilibrium concentration with respect to calcite and the in the cave atmosphere. From these ingredients a numerical model of stalagmite growth into an equilibrium shape is presented. In this model one assumes idealistically that the water dripping to the apex flows continuously down the stalagmite, spreading out radially. By simple mass balance one finds that the equilibrium radius is , where is the volume of a drop and the drip interval. Furthermore numerical modeling repro­duces the vertical shifting of the stalagmite’s equilibrium shape. Finally an interesting similarity rule is found. If one scales two stalagmites of differing to the same size and chooses their growth axes as common axis and their apexes as common ori­gin, both show identical shapes. In other words regular stalag­mites are similar geometrically. This similarity rule is verified by digitizing the shapes of various natural stalagmites with di­ameters between 5 cm and 20 m. Within small natural varia­tions, the rescaled shapes are identical and close to the shape of the numerical model.